Что такое четырёхмерное пространство?

Существуют 2 различных понятия, которые называют четвёртым измерением и часто их путают друг с другом. Чаще всего под четвёртым измерением понимают время. Такая система отсчёта, где 3 пространственных измерения и одно временное называют четырёхмерным пространством-временем Минковского. Такая система отсчёта удобна в физике, особенно в специальной теории относительности. Но помимо четырёхмерного пространства-времени Минковского есть ещё один вариант четвёртого измерения, где 4 пространственных измерения без учёта времени. Время в таком определении четвёртого измерения вообще не учитывается, а вводится понятие о дополнительном пространственном направлении. Именно об этом и пойдёт речь в данной статье.

Какими свойствами обладает пространство?

Пространство обладает такими свойствами, как размерность, форма и кривизна. Помимо этого положение в пространстве математически можно выразить через координаты, которые прямо зависят от размерности пространства. Размерность пространства Вселенной, в которой мы живём равна трём, кривизна различается рядом с разными объектами, обладающими гравитацией, а вот форма неизвестна.

Как проявляется кривизна пространства? 

Кривизна пространства проявляется рядом с массивными телами. Рядом с ними пролетающие мимо объекты искажают направление своего движения. К примеру, луч света, который движется всегда по прямой, рядом с массивным телом начинает отклоняться от прямолинейного движения. И луч света при этом не притягивается к массивному телу. Искажается именно направление движения. И чем плотнее и массивнее тело, тем сильнее прямолинейное движение будет искривляться в сторону центра масс массивного тела.

Источник: i.sunhome.ru

Грубо говоря, гравитация ничего не притягивает, она является просто искажением направления движения тела. Причём движение само по себе тоже на самом деле не меняется. Прямая так и остаётся прямой. Искривляется само пространство в котором эта прямая как и была прямой, так и остаётся, но из-за искривления пространства в котором проходит эта прямая мы видим и отклонение направления движения по этой прямой. Гипотетическая концепция варп-двигателя строится на возможности искусственно искривлять пространство сжимая его спереди, и расширяя позади. Само тело при этом остаётся неподвижным. Ограничений на скорость искривления пространства в отличии от ограничения на скорость передвижения в пространстве нет. Поэтому чисто гипотетически искривляя пространство можно изменить положение тела быстрее скорости света.

Что такое форма пространства?

Какие последствия могут быть от разной формы пространства Вселенной? 

Пространство всей Вселенной обладает ещё и формой. Какая она именно - пока не известно. Но наиболее вероятны 3 варианта - плоское, сферическое или седловидное. Как известно, Вселенная расширяется и в зависимости от формы пространства Вселенной возможен разный итог истории всей Вселенной. Если пространство нашей Вселенной плоское, то два параллельных луча, испущенных из двух точек в пространстве всегда без стороннего влияния будут параллельны. Расстояние между этими двумя лучами везде будет одинаково, и даже если бы Вселенная не расширялась два луча света никогда не вернутся в точку из которой начали движение. Если пространство нашей Вселенной плоское, то в далёком будущем Вселенную ожидает тепловая смерть. Вселенная просто придёт в состояние термодинамического равновесия.

Второй вариант возможной формы пространства Вселенной - сферический. Если пространство нашей Вселенной сферическое, то два параллельных луча, испущенных из одной точки так же всегда будут параллельны, если на них не будет оказываться стороннее влияние. Так же, как и в плоской Вселенной. Но, если не учитывать расширения Вселенной, то в сферической Вселенной лучи света, испущенные из одной точки через очень большой промежуток времени вернутся в точку из которой они начали движение. При таком сценарии, если учитывать время, момент Большого взрыва является полюсом условной сферы, Вселенная расширяется сначала с ускорением, как срез этой сферы, который движется от полюса к "экватору". Но затем после достижение условного "экватора" расширение Вселенной замедлится, после чего начнётся большое сжатие и условный срез начнёт движение от "экватора" к новому "полюсу" и всё закончится сжатием в одну точку, после чего последует новый Большой Взрыв и так будет происходить снова и снова. Третий вариант возможной формы Вселенной - седловидный. При таком варианте параллельные лучи без стороннего влияния со временем начнут расходиться и лучи света тоже никогда не вернутся в исходную точку. Если пространство нашей Вселенной имеет именно такую форму, то расширение Вселенной будет ускоряться всегда и в конечном итоге Вселенная закончит своё существование Большим Разрывом. Когда распадутся галактики, планетные системы, сами планеты, и даже атомы.

Что такое размерность пространства?

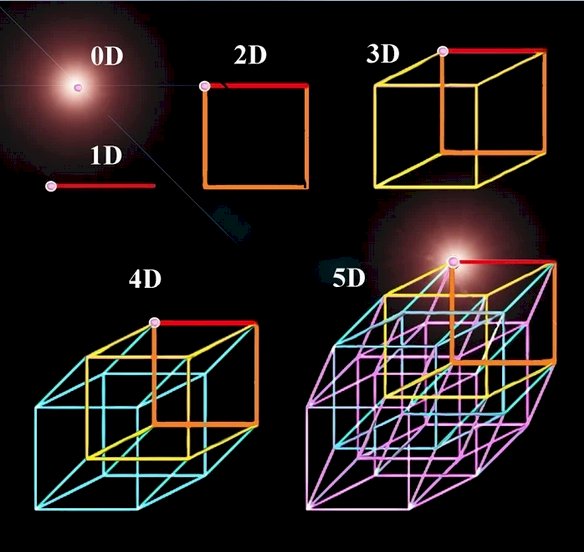
С кривизной и формой пространства разобрались. Последнее свойство пространства, о котором пойдёт речь - его размерность. Размерность - это количество независимых параметров, необходимых для описания состояния объекта, или количество степеней свободы системы. Например в 0-мерном пространстве таких параметров нет вообще. 0-мерное пространство - это точка. В нём нет никаких величин. Ни размеров, ни форм, ни направлений. В одномерном пространстве появляется один параметр, который в координатах можно обозначить, как х. Одномерное пространство грубо говоря представляет из себя линию. В нём можно двигаться вперёд/назад. В нём возможны отрезки разной длины. Появляется понятие размера, и направления. При изменении параметра х в большую или меньшую сторону можно перемещать точку в таком пространстве вперёд или назад. Любопытно, что одномерный отрезок любой длины в таком пространстве можно разрезать на бесконечное количество более мелких отрезков. Иными словами отрезок любой длины включает в себя бесконечно много точек. В одномерном пространстве невозможно вращение. В двухмерном пространстве появляется вторая независимая величина, которую в координатах изображают, как у. И есть две независимые величины - х и у. В двухмерном пространстве появляется возможность провести перпендикуляр. Два отрезка могут быть перпендикулярны друг другу. Появляется понятие формы и вращения. Теперь положение точки в пространстве может не только меняться по величине х или у в определённых случаях, но также они могут быть взаимозависимы, и при определённом стечении обстоятельств значение величины х меняется на значение величины у и наоборот, что описывается матрицей поворота. У двухмерных объектов появляется 2 величины - длина и ширина, один вариант поворота - ху, и два варианта взаимно перпендикулярных направлений - вверх/вниз, и вправо/влево.

Трёхмерное пространство включает 3 независимых величины - х, у, z. Пространство нашего мира, в котором мы живём как раз трёхмерно. Предметы обладают тремя величинами длиной, шириной и высотой. Появляется 3 варианта вращения - xy, xz, yz. В трёхмерном пространстве существует 3 взаимно-перпендикулярных направления - вверх/вниз, влево/вправо и вперёд/назад. Двухмерные предметы плоские по третьей величине, потому, что две величины ненулевые, а третья величина близка к 0, поэтому по третьей величине двухмерные предметы являются плоскими.

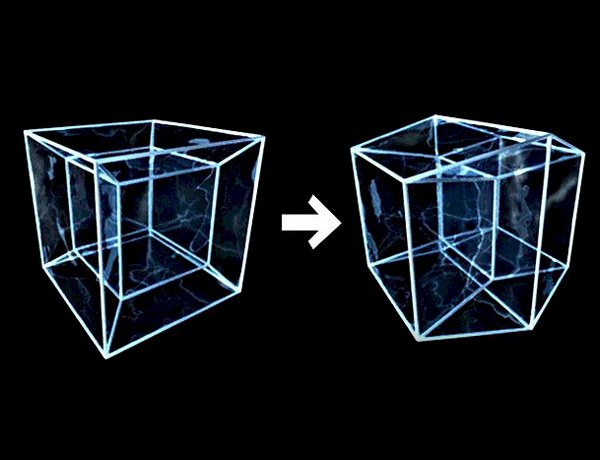
Теперь переходим к самому интересному. К четырёхмерному пространству. Такое пространство обладает четырьмя независимыми величинами и точки в пространстве обозначаются в координатах четырьмя значениями - x, y, z, w. В таком пространстве есть 4 взаимно перпендикулярных направления. Напомню, в нашем трёхмерном пространстве невозможно провести 4 взаимно перпендикулярных линии, а в четырёхмерном пространстве можно. Как это всё выглядит, можно посмотреть вот в этом видео:

Соответственно четырёхмерные фигуры обладают четырьмя величинами - длиной, шириной, высотой, и ещё одной, которую в некоторых источниках назвали густотой (хотя это просто название, её можно было назвать как угодно). Четвёртая величина у трёхмерных предметов равна 0, поэтому трёхмерные предметы в четырёхмерном пространстве будут плоскими при развороте таким способом, чтоб было видно четвёртую сторону. В этом видео: 

показана модель трёхмерного человека в четырёхмерном пространстве. В таком пространстве, кстати, уже существует 6 степеней вращения - xy, xz, yz, xw, yw, zw. Вообще количество степеней вращения в пространствах с разной размерностью вычисляется по такой формуле: N = (k * (k - 1)) / 2, где N - количество степеней вращения, а k - размерность пространства. К примеру, для 2D количество степеней вращения будет (2 * 1) / 2 = 1. Для 3D - (3 * 2) / 2 = 3. Для 4D - (4 * 3) / 2 = 6. И т.д.

• Двухмерные предметы обладают площадью.
• Трёхмерные - объёмом, и их можно разрезать на двухмерные срезы.
• Четырёхмерные предметы можно разрезать по четвёртой величине на трёхмерные срезы, которые будут объёмны по трём величинам и плоскими по четвёртой. 

Сами четырёхмерные предметы обладают четырёхмерным гиперобъёмом. К примеру в основании трёхмерного цилиндра лежат двухмерные кружки. А в основании четырёхмерного цилиндра лежат трёхмерные сферы, которые можно вращать в трёх измерениях, как трёхмерную сферу, и в четвёртом измерении развернуть, как цилиндр. Как это выглядит можно посмотреть в этом видео:

Иногда при взгляде на вращение в четырёхмерном пространстве может создаться впечатление, что фигура выворачивает наизнанку. На самом деле это не так. То, что кажется, что находится внутри четырёхмерной фигуры - на самом деле находится не внутри, а вдали по четвёртой величине. Вот в этом видео хорошо показано чем отличается к примеру настоящий четырёхмерный куб (тессеракт), от трёхмерного псевдотессеракта, который представляет из себя трёхмерный куб внутри которого куб поменьше:

Ещё одно замечание, которое часто делают при виде четырёхмерного пространства, это то, что мы видим не само четырёхмерное пространство, а лишь его проекцию на двухмерный экран. Тем не менее, учитывая особенности нашего зрения, окажись мы в реальном четырёхмерном пространстве, мы бы его видели так же, как и на экране. Благодаря этой самой проекции, мы на двухмерном экране воспринимаем трёхмерные игры практически так же, как и реальный мир. При проекции четырёхмерного пространства на третье измерение мы бы при съёмках этой проекции видели бы так же на экране, как и оператор, который снимает эту проекцию. Ну и глаза у нас находятся в одной плоскости, что обеспечивает нам двухмерную картинку. Хотя мы и способны определять расстояние, что обеспечивает нам некоторую трёхмерность зрения. Тем не менее отсутствие бинокулярности при проекции не сильно бросается в глаза. И в целом в реальном четырёхмерном пространстве мы бы видели практически так же, как и на экране. Разве что могли бы ещё оценивать расстояние до двухмерных предметов.

В четырёхмерном пространстве возможны 2 вида тора (бублика). Один из них - аналог трёхмерного тора. Другой - уникальный, так как является симметричным, чего невозможно сделать в нашем трёхмерном пространстве. Посмотреть на 2 вида четырёхмерного тора можно в этом видео:

В целом пространство может обладать любой размерностью. А на этом у меня пока всё.